![]()
Current version 2a
New Features:
Now accurate (to within one degree) for up to 36 days after syncing.
User can select the # of days data to store (12, 24, or 36). Displays how many days left.
User can select which objects to store (in order to reduce storage requirements). Planets may be stored either as fixed object (requiring only 1 record) or as moving objects (requiring 2, 3, or 4 records depending on # of days selected).
One can scroll through the objects on the watch much more quickly (waits a second before computing so you can rotate the crown to the next object).
Fixed a bug regarding Daylight Savings Time (in Libnova) and also allowed manual entry of user time zone (just in case the system gets it wrong).
Automatically recalculates and updates every 15 seconds.
Calculates horizontal coordinates (azimuth and altitude) of Sun, Moon, all the planets and a few celestial objects and displays them graphically.
User must enter his longitude and latitude through the dll interface of the Timex software. The selection of objects and #days is also made there.
Object's symbol is shown in upper left and name is shown in upper right.
Polar plot on left flashes position. North is up, overhead is in the center.
Azimuth (A:) and elevation (AKA, altitude, E:) are shown on the right side. Azimuth is from 0 to 360 degrees with 0 being North, 90 is East, 180 South, and 270 West. Elevation is from -90 to 90 with 90 being straight up, 0 being on the horizon, and -90 being straight down.
You can rotate the crown to cycle through the objects.
Push space to see a text note about the object.
The object's coordinates at noon of the day of syncing are sent to the watch. So, fast moving objects (like the moon) will have some error associated with it's position.
Download the source code for the Windows dll here.
How it works (for version 1a)...
The dll file for this app (StarFind.dll) inputs the users geographic coordinates (longitude and latitude). It also gets the date from the host computer. It uses the Libnova library to calculate the Julian date corresponding to noon on the current date. It then uses Libnova again to calculate the GMST (Greenwich Mean Sidereal Time) for this Julian date. It then uses Libnova to calculate the equatorial coordinates (RA and DEC) for the sun, moon, and jupiter for the previously mentioned Julian date. This data is all stored on the watch as database records with the following format:
The wristapp then has to calculate the horizontal coordinates (azimuth and altitude) based on this input (longitude, latitude, GMST at noon, and the RA&DEC of the object) and the watch's time. Here are the details:
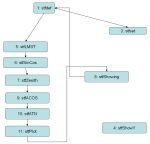
State 1 (stfDef): Opens database and loads longitude, latitude, and GMSTNoon. It then ensures that the currently selected object is valid and loads it's RA and DEC. It also displays the objects symbol and name and loads it's text message into a buffer for later display.
State 5 (stfLMST): Gets the current time from the watch. Calculates #minutes since midnight. Converts this to a floating point number. Subtracts 720 minutes (12*60) to get #minutes since noon (can be negative). Multiplies by 1.0028 to convert to sidereal minutes. Multiplies by 0.25 (360/(24*60)=1/4) to convert minutes to degrees. Adds GMSTNoon. Subtract longitude. Now have LMST (local mean sidereal time)! Then, subracts RA of object to get the HA (hour angle) of the object.
State 6 (stfSinCos): This state has the code to do Sine and Cosine of an angle. First calculates and stores sin(HA) so we can later tell if object is east or west. Then, calculates cos(HA), cos(LAT), cos(DEC), sin(LAT), sin(DEC) and stores all these for later.
State 7 (stfZenith): This state calculates the cosine of the objects zenith and azimuth angles it has square root code to get cos(alt) from cos(zenith). Uses cos(zenith)=sin(dec)*sin(lat)+cos(dec)*cos(lat)*cos(HA). To calculate cos(azimuth), first does cos(alt)=sqrt(1-cos(zenith)^2). Then, does cos(azimuth)=(sin(dec)*cos(lat)+cos(dec)*sin(lat)*cos(HA))/cos(alt). Then does sin(azimuth)=sin(HA)*cos(DEC)/cos(alt).
State 9 (stfAcos): Takes first step toward calculating the inverse cosine
of cos(altitude) and cos(azimuth) by doing the x/sqrt(1-x*x) part. This state also has square root code.
State 10: (stfATN): Finishes up calculating altitude and azimuth angles by doing the pi/2-arctangent(x) part of the calculation started in state 9. This state is taken up by a lot of code to do the arctangent function.
State 11: (stfPlot): This state plots the position in the polar display and writes the azimuth and elevation angles to the screen. First, it makes sure elevation (AKA altitude) is <90 degrees. If bigger, we subtract 180 and show it as negative. Then we calculate the polar position via: x=9+8*(zenith/90)*sin(azimuth), y=6-5*(zenith/90)*cos(azim) and converts x and y to an integer. We then convert azimuth angle to an integer and correct for sign (if sin(HA) is positive then azimuth=360-azimuth) and show on line 1. Then calculate Altitude=90-Zenith and show on line2.
State 8: (stfShowing): This state just prints "A:" and "E:" on the screen for azimuth and elevation and blinks the star location on the chart. It also shows the object's message if user pushes the start button. If the user rotates the crown, the current object number is incremented and we go back to state 1.
Another state (State 4: stfShowY) is used only for debugging, not in application.
State Diagram:
Memory Usage:
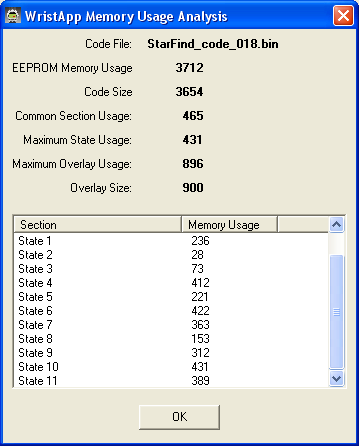
As you can see, the overlay usage is nearly maximum.